This is the second post in a three-part series. Read the first post, “Why Smart People Are Not Always Rational” and the final installment, “Why Smart Doesn’t Guarantee Rational, Part III.”
In a previous post I discussed the fascinating case of Paul Frampton who, as the website News Observer put it, “instantly was transformed from superstar particle phenomenologist with three Oxford University degrees to international tabloid fodder” when he fell for a honey trap drug smuggling scam. In it, I talked about irrationality in Mensa, the “high IQ society”, and the fact that rational behavior is not, as most of us assume, a direct product of intelligence.
If rationality is not a product of intelligence, then what is it a product of?
To find out, researchers such as Keith Stanovich, Richard West, and others have studied individual differences in rationality. In other words, they have worked to identify what makes people who perform well on a specific set of cognitive tasks different from people who do not. Intelligence is one factor, but it does not explain all of the variability. There are some tasks for which performance is not related to intelligence much at all.
This is surprising to most, because we tend to think of the term “smart” somewhat simplistically. We expect people who are smart in one way to be smart in every way. But that’s not quite how intelligence works (again, please read my first post, which discusses the differences between IQ and rationality, and how each is measured).
So what’s going on?
Well, after many years of study, Stanovich and others have identified a number of factors which explain these differences, but I think the list can be collapsed into four general categories: intelligence, knowledge, need for cognition, and open-mindedness. Or, if you prefer my casual references, we can be irrational because we are stupid, ignorant, lazy, arrogant, or some combination of those.
Intelligence can be thought of as cognitive ability, or the ability to perform a specific set of cognitive tasks. It is an important factor in rational thought, but it is only one factor that matters. Knowledge is necessary to solve many problems and intelligence cannot make up for a lack of information.
But the other items are thinking dispositions. More specific examples of thinking dispositions are long-term thinking (about future consequences), dogmatism, and superstition. Thinking dispositions are rooted in goals, beliefs, belief structure, and attitudes about beliefs—toward forming and changing beliefs. Goals and attitudes involve values, so it should not be surprising that beliefs often do, too.
To be rational, we must know when to override our default thinking, then we must do it. Knowing when to override involves intelligence and knowledge, but the will or motivation to do so is another thing altogether. That requires more than critical thinking, more than problem-solving ability. It requires us to hold our current world view in a kind of escrow while we consider an alternative view in an open-minded fashion. Some thinking dispositions get in the way of that process.
Need for cognition is one of the dispositions that can help or hinder rational thought. Overriding default thinking requires energy, and human beings are natural cognitive misers. What that means is that we will spend as little energy as necessary to meet our goals. People vary in how much they are willing to spend. The more curious and interested one is in spending time and energy in finding the correct answer or best choice to meet one’s goals, the more rational one will be.
For example, consider the following problem:
Jack is looking at Anne, but Anne is looking at George. Jack is married, but George is not. Is a married person looking at an unmarried person?
Your options are:
- Yes
- No
- Cannot be determined
If you are like most people, you answered “3″. However, the correct answer is 1. This becomes obvious if you approach the question in a way that is not intuitive. Most people notice that they know nothing about Anne, see that they have an option for “cannot be determined” and stop there. However, when we take that third option away, the typical answer is a correct one. People do what they need to do to find an answer: they consider the possibilities.
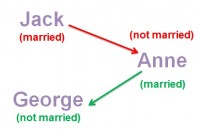Anne must be either married or unmarried. If she is married, she is looking at an unmarried person, so the answer is “yes” (the green path). If she is unmarried, then the answer is still “yes” because a married person is looking at her (the red path). In the end, it doesn’t matter what we do and do not know about Anne’s marital status.
How well people perform this task under controlled conditions is related to the need for cognition–how much energy one is willing to expend to find the best answer. This can be an important factor in real life situations such as policy-making. For example, it might seem like a wonderful idea to raise high school graduation standards in order to ensure that all graduates qualify to attend college. However, the long-term consequences of such a policy might include things like grade inflation and lower graduation rates. Thinking things through more thoroughly can reveal some interesting problems with what seems like a great idea on the surface.
Most people are surprised to discover that former president George W. Bush is not stupid. His IQ has been estimated consistently at around 120, which is well above average. However, he has a reputation for making poor, irrational choices. Even many Republicans have alluded to his lack of intellectual curiosity. This deficit of the need to think things through renders intelligence useless and leads to irrational choices and behaviors. To illustrate the gravity of this problem, consider the following experiment.
Participants were asked to allocate 100 livers to 200 children who needed transplants. The children were divided into Group A and Group B, each with 100 children. The participants did what you probably expected: they gave half to each group. But in a follow-up study, the participants were told that the children in Group A had an 80% chance, on average, of surviving the surgery and the children in Group B had a 20% chance. If the goal of liver transplants is to save as many lives as possible, something I think we can all agree is more important than giving hope (in this case, we cannot do both because there are not enough livers), then the choice is clear: allocate the livers to those most likely to survive. This makes giving any livers to children in Group B an irrational choice.
However, only 24% of participants in this study chose to give all of the livers to Group A. More than a quarter of the participants gave half of the livers to Group B.
The difference between these two choices is 30 dead children.
When asked why they chose to give so many of the livers to the children in group B, participants gave answers such as “I would like to give hope to the Group who has the least chance of survival.” One said, “I believe in God. God doesn’t work in numbers.”
Now, you might be tempted to accept those answers and think that emotion and compassion got in the way of better thinking, not “cognitive laziness”. But scientists like truth and truth isn’t always pretty, so another experiment was conducted to test these excuses. In this one, the 200 children were ranked, individually, from the highest probability of survival to the lowest. If the reasons given for allocating to Group B were accurate, we’d expect at least some of the participants to distribute the livers somewhat evenly, as some did in the previous study (the distribution on the left below). However, the participants in this study had no trouble allocating the livers to the top 100 patients when they were not grouped (the distribution on the right below.
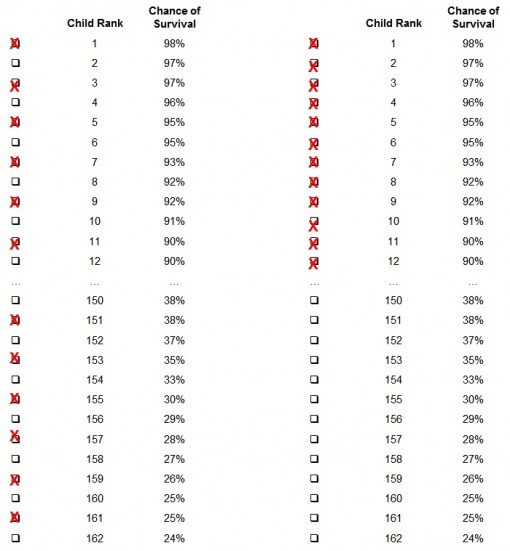
The comments about wanting to give hope to the children less likely to survive were justifications for what amounts to lazy thinking. The way the question was framed determined how people responded, not their real preferences, their real goals. Their goals and preferences changed to justify the behavior.
And the result, were this a real-life situation, is the death of children who might otherwise have survived.
To summarize so far, we are sometimes irrational because we are stupid (unintelligent) and we are sometimes irrational because we are ignorant (lack knowledge), but we are often irrational because we are lazy (lack intellectual curiosity) or arrogant. That last category, open-mindedness (including arrogance/overconfidence) I will save for a third post on the subject. In the meantime, there are a couple of take-home messages I would like to end with:
- We all believe that we are rational. We all think that our choices and actions are the result of good thought processes. We recognize that human beings are naturally irrational, but we all seem to think that “human beings” means “other people”. Think about what you believe makes you different. You have to get beyond, “I’m smart”, but you also have to get beyond “I use logic and reason”, because we all think that we are using logic and reason, yet few, if any, of us are consistently rational. This information should be used as a mirror as much, if not more, as it is used to understand others.
- To paraphrase Keith Stanovich, when we allow our dispositions and intellectual laziness to keep us from deeper thinking, when our decisions are determined, not by what we want, but by how the choices are presented, we relinquish our power to those who frame the questions.
Rather than include a very long list of academic literature, I will instead recommend the following books, as most of the literature referenced in these posts is covered in at least one of them:
Stanovich, K.E. (2010). What Intelligence Tests Miss: The Psychology of Rational Thought. Yale University Press
Kahneman, D. (2011). Thinking, Fast and Slow. Farrar, Straus and Giroux
Ariely, D. (2009). Predictably Irrational. Harper
Tavris, C. & Aronson, E. (2007). Mistakes Were Made (But Not by Me): Why We Justify Foolish Beliefs, Bad Decisions, and Hurtful Acts. Houghton Mifflin Harcourt
Read the final installment of this three-part series, “Why Smart Doesn’t Guarantee Rational, Part III.”
Where is the third part?
it is leveraging the risk of having a wrong estimate of chance of survival.http://larsjaeger.ch/
As long as the estimate is better than a coin flip, it favors giving all the livers to the 80% group. Even if the actual chances of survival for the two groups turn out to be 51% vs. 49%, you’d still save more lives by giving all the livers to the 51% group. Heck, even if it WAS a coin flip, then giving all the livers to one group would save as many lives as giving half the livers to each group.
Love this article, posted it to my Facebook. I am, however, too inetllectually lazy or preoccupied to process the math in these comments, since I don’t have any pressing need. This seems to me to be the most rational approach for the moment?
I’d like to suggest adding to the dispositions affecting rationality? There are few motivators greater than fear. People are often disinclined to think deeper for fear of what they might find. It doesn’t quite fit the description of arrogance, though it almost always looks like it by the time the behavior spins off.
There are the intellectualy lazy, the indifferent and the curiosity impaired. There are the truly arrogant born of narcissistic tendencies or ignorance or both. Then there are the fearful that shield themselves with a facade of arrogance, because we are also often afraid to admit that we are afraid.
Never mind. Courage would be a component of open mindedness. One cannot be a coward and be open minded.
The list of components that Stanovich has come up with is much longer than the four I’ve listed, but I believe that most of the times fall into these four categories. And, yes, I’d put that kind of fear/denial falls into the category of how open/closed minded one is.
I feel that the example on the marital status of Anne is oversimplistic and encourages dualistic thinking. Insisting that the correct answer is 1 ignores the fact that there are other possibilities of Anne’s marital status, e.g. divorced, widowed, separated, or perhaps just ‘It’s complicated’. In any case, Anne’s maritial status is no one’s business but Anne.
:)
Divorced or widowed is not married. Married but separated is married.
The problem with smart people is that there is no easy answer to any problem. I do not believe there exists such a thing as 20% and 80% chance of survival for 200 children. How could anybody measure that so precisely and not be able to take a decision himself? Obviously the person asking the problem is trying to influence me. Therefore I don’t trust that person and I give 50% to each group because it is leveraging the risk of having a wrong estimate of chance of survival. To me, the most influential factor is trust. Not laziness.
Maybe it’s all a lie and the children don’t even need liver transplants. Don’t give them any livers.
Shift the goal — heartlessly, I admit — from maximizing children saved to minimizing the number of angry parents, and the irrational group is probably making the best choice. E.g.: You are a heartless policymaker. You have 100 livers, 200 dying children in Group A and B. Group A donors will have an 80% survival rate; Group B, 20%. How can you allocate the livers in such a way as to minimize the number of parents who are angry at you?
While the question no longer has an empirical answer, it’s fairly likely the 50-50 split is most likely to minimize the number of angry parents. People consider fairness very important, and to some parents in Group A the decision will appear fair; any parents who got a liver probably won’t be angry at you, the policymaker, even if the kid dies. Moreover, the people in Group B got livers, taking the wind out of their sails. Not many parents in Group B will want to argue Group A should have gotten even more livers. So you let 30 kids die for your own benefit.
Do irrational beliefs empower people to make decisions that hurt others and benefit themselves?
I take all the livers and make soup.
Returning to the question about livers.
But wouldn’t giving all the livers to 80% survival group make us more ruthless? Wouldn’t it stop us from searching a better solution where all the lives are saved? If you accept the idea that you will have to kill somebody to save somebody’s live, wouldn’t it become an easy way out when other options are available? Wouldn’t people still kill wen in fact it’s possible to save all lives? Absolutely for the same reason – for lazy thinking. We will kill somebody to save somebodys’ lives just because we will be to lazy to search for better solution, to save all lives.
Did you make such kind of experiment? Wouldn’t such people (who gave all to “80%” group) be more immoral in real life and lead to much more destructive consequences, losing more lives, then those who separated equally and are more interested in saving *everybody*, not just saving the most?
I think, there’s also confusion between “surviving the operation” and “allocating the liver”. If you put question “Will you make operations to the group which is 20% likely to survive it or to the group that is 80% likely to survive it, when you have only 100 operations and survival rate without operation is not known. How much operations would you give to each group?” (in your question it’s not stated what is chance of survival without the operation), then people might chose to allocate everything to “80%” group more often.
“But wouldn’t giving all the livers to 80% survival group make us more ruthless?”
As opposed to giving half the livers to the 20% survival group, resulting in more dead children? There aren’t enough livers for everybody, so no allocation will save everybody. Wouldn’t the intellectually lazy bleeding hearts (who give half to the 20% group because it feels better) be more immoral in real life, leading to more death and destruction while patting themselves on the back for their good intentions?
But what we are all striving for is wisdom, which presumably is the product of intelligence, rationality, experience and judgement. Or is it?
“Wisdom”, at least in the psychological literature, is largely considered to be a product of experience. An excellent book on the topic, if you’re interested, is Schwartz and Sharpe’s “Practical Wisdom”.
I contest the idea that splitting the livers between each group no matter the survival rates of the two is lazy, I’d suggest the allocating of the livers to the top contenders of the groups put together is actually lazier. In my case, asking me to imagine two groups of kids creates an empathy with these imagined children and the choice of splitting the livers is all about removing my responsibility for killing off an entire group of them, imagined or not. But with just one group you know that half of them will not be receiving an organ donation, the moral responsibility of choice is removed when you allocate it to the top contenders, you’re not condemning a group, you’re making a rational choice. As a test for rationality, sure it may work, but it’s not laziness that produces different results.
the second experiment (liver dilemma) has a fundamental problem. you can not decide with one measures of central tendency (e.g. average). it is flawed because of ecological fallacy
all the children can be saved , it does not take an entire kidney to to regrow a healthy kidney
The question is about livers, but of course that doesn’t matter. It’s a thought experiment; people with no medical background are not likely to be asked to allocate livers for transplants.
Arrogance is one of the listed predictors of susceptibility to logical fallacy. Knowing one’s elevated IQ score, and believing this confers a sort of invulnerability from delusion, is a common delusion. The other indicators can remain hidden for a spell but arrogance based upon one’s superior IQ score reveals itself almost instantly.
Thanks for ruining this article with the political garbage. I was planning on linking it to my website until I came across that.
Great post, thank you!
I read this article because I consider myself smart but make bad choices, especially with money, ALOT. It got me thinking about why and maybe selfishness is a good reason?
An important piece of understanding is that in the real world (outside of math) there are no right answers as most questions involve levels of compromise. Higher levels of experience (usually with age) teaches us to look for the pluses and minuses in each situation. The choice of best or least worst solution is always biased by the weight we assign to pluses and minuses based on our value system. Thus people who are equally intelligent, knowledgeable, lazy and arrogant can choose different “right” answers. Researchers can also fall into the trap of assuming that they know the right answers. What blind spots or biases are we ignoring or explaining away? The ability to understand a situation from many angles is beyond simple open mindedness. Intelligence and intense curiosity are also required to hold opposing viewpoints in one head as there may be no right answer.
Looking forward to part 3 as overconfidence is a common trait in academia.
Being able to apply the knowledge is an important part of intelligence. About half of Mensa members can do and that’s all. I talked to the president of Athiests United and he said the same thing. Mensa sends members to AU for exposure. I’m lucky, that gene showed up with me. Half of these Mensa people DONT have this trait, so they’re really not as smart as everyone thinks they are. A simple DNA scan in the near future will bear this out. Carl Sagan lamented this in his book “science as a candle of light”. As a good example, educated people who still have all sorts of ridiculous superstitions. That’s ineptitude, plain and simple.
I think my mother summed it up better. “There’s no fool like an old fool.” A piece of old folk wisdom that is for once – wise.
Max, Schwartz emphasizes that neither category of people make bad decisions. I think his point is that a satisficers are not “the types of impulse buyers exploited by scammers”.
And I don’t buy it. The WSJ article gives a couple of examples:
1) Mr. Richard, 39, a marketing professor and public relations executive, decided the couple needed a new car to replace their old one. He spent a few days researching SUVs, found a good deal on an Audi Q5 and signed the lease—without telling his wife.
“I knew that bringing her into the conversation about it up front was going to take way too long, and we would miss the deal,” he says. “So I pushed the button.”
2) Rob Ynes creates spreadsheets when he makes major decisions. His wife, Mary Ellen, prides herself on being able to decide on a new car, children’s names—“Even shoes!” she says—with little or no deliberation. “I see it, I consider a few options and bam!—within minutes, a decision and most likely a purchase is made,” says Ms. Ynes, a 50-year-old public relations representative in Redwood City, Calif.
Ironically, both satisficers in these examples are in marketing/PR, so they might not fall for marketing tricks like special limited time offers that seem designed for people like themselves. Telemarketers do not like maximizers who create a spreadsheet and sleep on it.
You can’t judge a whole body of research based on the choices of examples made by a WSJ-journalist. Besides, neither of the examples you picked gives any indication of not having high standards.
I don’t know if this is a wide body of research or one biased researcher. Is this the same as the research on perfectionism? The WSJ article tried to make satisficers look good, but they still came off as people who make rash decisions “with little or no deliberation” and avoid feedback from others. Satisficers have lower standards by definition. As Schwartz said, “Maximizers are people who want the very best. Satisficers are people who want good enough.” His maximizer test includes the statement, “No matter what I do, I have the highest standards for myself.”
But if satisficers do in fact make equally good decisions, then how does that square with Barbara’s point that, “This deficit of the need to think things through renders intelligence useless and leads to irrational choices and behaviors”? Do satisficers think things through even though they have lower standards and make decisions with little deliberation?
Max, with all respect you are being a little shy of rational on this one. “By definition” is a logically fallacious argument. Here, have a link:
http://lesswrong.com/lw/np/disputing_definitions/
There’s plenty more on the subject of you want it.
Now, to the point on thinking things through. There is a huge discussion to be had on what constitutes a “good decision”. There most certainly exists an argument that a decision without significant detrimental outcomes that satisfies the criteria and leads to happiness would be a pretty damn good decision. If I can get (say, for example) 90% of the return for (maybe about) 10% of the effort, and I end up very happy with my decision, did I not make a good decision?
You seem to be confusing “good” with “objectively optimal”, and they are very clearly two quite different propositions.
Yeah sure, satisficers have high standards, introverts are outgoing, black is white, good is bad… That’s rational, that’s less wrong.
Good decision means objectively good, regardless of the effort that goes into it. Getting ripped off is objectively bad even if you think you got a good deal. Because in that case “our decisions are determined, not by what we want, but by how the choices are presented.”
I wouldn’t object if Schwartz had said that satisficers make objectively worse decisions, but end up feeling better about them and spend less time deliberating. But he made it sound like there’s no downside to it.
It’s a pretty robust body of research. I recommend reading the book, which covers a lot of that research, before judging.
http://www.amazon.com/dp/0060005696/ref=tsm_1_fb_lk
So I read this in the WSJ
“‘Maximizers’ Check All Options, ‘Satisficers’ Make the Best Decision Quickly: Guess Who’s Happier”
http://online.wsj.com/articles/how-you-make-decisions-says-a-lot-about-how-happy-you-are-1412614997
“Maximizers are people who want the very best. Satisficers are people who want good enough,” says Barry Schwartz, a professor of psychology at Swarthmore College in Pennsylvania.
In a study published in 2006 in the journal Psychological Science, Dr. Schwartz and colleagues followed 548 job-seeking college seniors at 11 schools from October through their graduation in June. Across the board, they found that the maximizers landed better jobs. Their starting salaries were, on average, 20% higher than those of the satisficers, but they felt worse about their jobs.
“The maximizer is kicking himself because he can’t examine every option and at some point had to just pick something,” Dr. Schwartz says. “Maximizers make good decisions and end up feeling bad about them. Satisficers make good decisions and end up feeling good.”
Dr. Schwartz says he found nothing to suggest that either maximizers or satisficers make bad decisions more often. Satisficers also have high standards, but they are happier than maximizers, he says. Maximizers tend to be more depressed and to report a lower satisfaction with life, his research found. The older you are, the less likely you are to be a maximizer—which helps explain why studies show people get happier as they get older.
Now, I can see how satisficers are happier with lower standards. What I don’t see is how “satisficers make good decisions” and have high standards, when by definition they don’t have high standards, and Schwartz’s own research found that they landed worse jobs, and they’re the types of impulse buyers exploited by scammers and telemarketers bearing special offers if you sign up right now.
I think that you are misunderstanding what Schwartz is saying. The difference between Maximizers and Satisficers is not a matter of standards in terms of what they are willing to accept, but in what they believe they can achieve. Maximizers don’t have a set standard, they just want the best available. Satisficers do have a set standard, and it could be a high one. But since all of our resources are limited, what Maximizers choose is limited to what they can afford or accomplish.
In the end, the Maximizer is less satisfied because they feel that they haven’t gotten the best, while the Satisficer is satisfied because they got what they wanted.
“The Paradox of Choice” is an excellent book (by Barry Schwarz) and I highly recommend it. It’s fascinating how we assume that choices make us happy when, in reality, the opposite tends to be true.
http://www.amazon.com/dp/0060005696/ref=tsm_1_fb_lk
Schwartz’s maximizer test includes the statement, “I never settle for second best.”
Sounds to me like a high standard of what maximizers are willing to accept.
Who’s more likely to be a lazy thinker and get the wrong answer on your logic puzzle, a maximizer or a satisficer?
Remember the game show Million Dollar Money Drop? Players start off with a million dollars, and scramble to allocate their money to four answers to a multiple-choice question. They lose the money they place on the wrong answers.
The optimal way to maximize winnings is to bet all the money on the most probable answer, yet players typically hedged their bets, taking money away from the most probable answer and betting it on less probable answers. I guess it’s loss aversion.
Loss aversion may be part of it. Another important factor is that the contestants may have a non-linear utility function.
If, for example, you reached the final question and you had a logarithmic utility function whose expected value you sought to maximize, your best play is to allocate your resources proportional to the probability of each answer.
Interesting. Can you show the math?
I don’t think I value money in a linear fashion, myself, though I’ve never thought about what sort of curve it might be. For small amounts, it might be linear, but for larger amounts, it’s not. If I were given the choice between $100 free and clear, or $300 if a flipped coin turns up heads, I’d easily take the chance on flipping the coin. If the amounts were $1,000,000 or $3,000,000, though, I’d take the million in a heartbeat. A million dollars would be life-changing for me, but three million would not be three times more life-changing.
What if you could play the game ten times? Would you take $10 million or flip for up to $30 million?
If I could play the game ten times, then I’d do the coin flip. I could live with the approximately 1 in 6 chance that I’d walk away with less than the $10 million offer, because I’d be about 99.9% assured of walking away with at least $1 million.
This all has got me thinking about how, as many people I’ve heard argue, the world is stacked against the poor. A rich person would probably think I’m pretty stupid for taking a $1 million sure thing over a $1.5 million expected value, but it’s not the sort of opportunity that I would foresee a guy like me running into over and over.
Ok, I think I got it.
E(ln(x)) = p*ln(x) + (1-p)*ln(1-x)
dE/dx = p/x – (1-p)/(1-x) = 0
p/x = (1-p)/(1-x)
x = p
Let p in (0,1) be the probability that the answer is A and (1-p) be the probability that the answer is B.
Let M > 0 be the amount of money you have for the final round.
Let x be the share of your bankroll that you put on A.
Optimize the expected utility where the utility is logarithmic.
Then:
E = p ln(xM) + (1-p)ln[(1-x)M]
E = p[ln(x) + ln(M)] + (1-p)[ln(1-x) + ln(M)]
E = p[ln(x)] + (1-p)[ln(1-x)] + ln(M)
we briefly note that as x -> 0, ln(x) -> -oo and as x -> 1, ln(1-x) -> -oo
dE/dx = p/x – (1-p)/(1-x) = p/x – 1/(1-x) + p/(1-x) = [p(1-x) + (p-1)x]/[x(1-x)]
dE/dx = (p-x)/[x(1-x)] which has a zero only at x = p
d2E/dx2 = -p/(x^2) – 1/[(1-x)^2] + p/[(1-x)^2]
at x = p, d2E/dx2 = -p/p^2 – 1/(1-p)^2 + p/[(1-p)^2]
at x = p, d2E/dx2 = -1/p – 1/(1-p) < 0 for all p in (0,1)
therefore, x = p is a local maxima for E. Since this is the only interior critical point and the limits go to -oo, x = p is maximal when p is in (0,1). QED.
note: only in the case where p = 0 or p = 1 is our optimal wager x = 0 or x = 1 for a logarithmic utility.
Another utility function that works similarly is f(x)=1-(1-x)^2 = x(2-x), where x is between 0 and 1.
The expected value of it is the Brier score, which is maximum when x=p.
E(f(x)) = p(2x-x^2) + (1-p)(1-x^2) = 2px – px^2 + (1-p) – (1-p)x^2
dE/dx = 2p – 2px – 2(1-p)x = 2p – 2x = 0
x = p
d2E/dx2 = -2 < 0, so it's a local maximum
The most effective way to increase organ donation consent rates is to make it opt-out instead of opt-in.
“Do Defaults Save Lives?”
http://webs.wofford.edu/pechwj/Do%20Defaults%20Save%20Lives.pdf
This is fascinating to me. It ties in very nicely with work I’ve been reading on the tendency to stop looking for answers the first time you find a true answer or functional solution to a problem. I was struck by this the other day when I was considering the square root of 4. I’ve asked several people what the answer is and everyone has said 2. But -2 is also a true answer right? So it should be the set that includes 2 and -2, but people tend to exclude that longer answer because the first answer pops in their hand and satisfies the question.
Anyway, it’s a fascinating issue because many innovations are probably lost when people use “the way they know” and don’t consider better, more efficient alternatives.
No, it’s not. The square root of a is explicitly defined as the non-negative root of the problem x^2=a. But there are other similar math problems where you would get the same results, so the rest of the reasoning still holds.
I guess this is a case of point two: Irrationality due to lack of knowledge.
I am sorry but this is wong. Within the frame work of positive real numbers every number a has 2 square roots (e.g. +2 and -2 in the given example). The square root is defined as the solution to the equation x^2 = a. What you are talking about is the fact that there is only 1 positive root which is called the principal square root.
“In common usage, unless otherwise specified, ‘the’ square root is generally taken to mean the principal square root.”
http://mathworld.wolfram.com/SquareRoot.html
This reminds me of the phrases uttered atop Mount Stupid.
http://blogs-images.forbes.com/chrisbarth/files/2011/12/Mount-Stupid.gif
It’s a fine distinction, but it is not correct to say that -2 is a square root of 4. -2 is a solution to (root of) x^2=4, but the square root of 4 is 2.
I am sorry, but you do not get to define which answers are “correct”. The square root of two is not a number; it is a set. There are no one correct anwer. There are only elements and subsets of answers which are in or outside the set of possible answers.
Now, you can prove that 2 is the only positive integer answer in the set of possible answers, but you can also prove by contradiction that there are other answers. For instance, in the set of complex solutions, 2i+0 is also equal to the square root of two.
Now, in applied math, like physics, results that make no physical sense are wrong, but in pure mathematics, the correct answer is the entire set of possibilities, so unless you specify that you are restricted to the set of positive integers, claiming 2 is the root 4 is in error.